选课程 



- 选课程
- 查院校
- 查专业
- 找资讯
400-108-7500

在考研数学中, 关于连续函数在闭区间上的性质有 4 个经常用到的定理, 它们分别是: 最 值定理, 有界性定理, 零点定理, 介值定理。其中关于连续函数的介值定理, 在很多高等数学 教材和考研复习资料上虽然都做了说明, 但都不是很完整, 导致很多学生在做这方面的习题时 产生混乱, 为了帮助广大考生完整透彻地理解介值定理, 启航考研数学辅导老师在这里向大家做一个完整的阐述, 供各位考生参考。
连续函数的介值定理按不同的条件和使用方法, 可以分为4种情况, 分别是:(m,M)上的介值定理, [m,M]上的介值定理, (f(a),f(b))上的介值定理, [f(a),f(b)]上的介值定理, 其中m,M分别为函数f(x)在闭区间[a,b]上的最小值和最大值, 此处假设f(a)f(b), 则相应地将区间改为(f(b),f(a))和[f(b),f(a)]。下面分别对这 4 种情况进行阐述。
定理一:
(m,M)上的介值定理. 设函数f(x)在闭区间[a,b]上连续,m,M分别为函数f(x)在闭区间[a,b]上的最小值和最大值, 则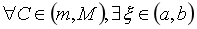 , 使得
, 使得
证明: 根据连续函数的最值定理得, , 使f(x1)=m,f(x2)=M,, 不妨设x1
, 使f(x1)=m,f(x2)=M,, 不妨设x1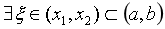 , 使得
, 使得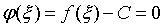 , 即
, 即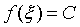 。
。

【26考研辅导课程推荐】:26考研集训课程,VIP领学计划,26考研VIP全科定制套餐(公共课VIP+专业课1对1) , 这些课程中都会配有内部讲义以及辅导书和资料,同时会有教研教辅双师模式对大家进行教学以及督学,并配有24小时答疑和模拟测试等,可直接咨询在线客服老师领取大额优惠券。
热门下载
资料下载
院校解析
真题解析
考研数学
考研英语
考研政治
考研备考