大连交通大学23研招初试考试大纲--601高等代数

2023年考研即将开始，希望23考研的考生根据大纲内容进行查漏补缺，24考研的考生可以根据大纲内容进行备考啦!以下是小编为大家整理的【大连交通大学--601高等代数】考试大纲具体内容，希望大家备考顺利哦~

科目代码：601

科目名称：高等代数

适用专业：数学类各专业

考试时间：3小时

考试方式：笔试

总　　分：150 分

考试范围：

一、多项式

1.多项式的带余除法及整除性;

2.多项式的因式分解、最大公因式、互素和重因式;

3. 不可约多项式的判定和性质;

4.多项式函数与多项式的根;

5. 复系数与实系数多项式的因式分解，有理系数多项式.

二、行列式

1.行列式的定义及性质;

2. 行列式按一行(列)展开;

3.运用行列式的性质及展开定理等计算行列式.

三、线性方程组

1.线性方程组的求解和讨论;

2.线性方程组有解的判别定理;

3.线性方程组解的结构及其解空间的讨论.

四、矩阵

1.矩阵的基本运算、矩阵的分块;

2.矩阵的初等变换、初等矩阵;

3. 矩阵的等价、合同、正交相似;

4.逆矩阵、伴随矩阵及其性质;

5.矩阵的秩，矩阵乘积的行列式与秩;

6. 运用初等变换法求矩阵的秩及逆矩阵;

7. 矩阵的特征值与特征向量，对角化矩阵.

五、二次型

1.二次型及其矩阵表示;

2.实数域和复数域上二次型的标准形与规范形;

3.正定二次型及其讨论.

六、线性空间

1.线性空间、子空间的定义与性质;

2. 向量组的线性相关性、极大线性无关组;

3. 线性空间的基、维数、向量关于基的坐标，基变换与坐标变换;

4. 生成子空间，子空间的交，子空间的和与直和、维数公式;

5. 线性空间的同构.

七、线性变换

1.线性变换的定义、性质与运算;

2. 线性变换的矩阵表示;

3.线性变换的核、值域的概念;

4. 线性变换及其矩阵的特征多项式、特征值和特征向量的概念和计算、特征子空间;

5.线性变换的不变子空间.

八、欧式空间

1.内积与欧氏空间的定义及性质，向量的长度、夹角、距离，正交矩阵;

2. 正交子空间与正交补;

3.欧氏空间的度量矩阵、标准正交基、线性无关向量组的Schmidt正交化方法;

4.正交变换与正交矩阵的等价条件，对称变换的概念与性质;

5.实对称矩阵的正交相似对角化的求法.

样 题 ：

一、(15分)f(x)∈P[x]，f(x)=f(-x)，如果(x-a)|f(x)，证明：(x²-a²)|f(x)

二、(10分)设f(x)=xⁿ⁺¹+xⁿ-2(n≥1)，求f(x)在有理数域上的不可约因式，并说明理由.

三、(15分)计算n阶行列式：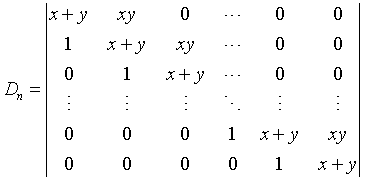

四、(20分)设n元非齐次线性方程组AX=β有解，且系数矩阵A的秩为r

证明：方程组AX=β的所有解向量中线性无关的最多个数是n-r+1

五、(15分，第1小题8分，第2小题7分)

设R⁴是由所有4维实行向量构成的线性空间，定义R⁴上的线性变换σ为σ(x₁,x₂,x₃,x₄)=(x₁+x₂,x₂-2x₃,x₃-3x₄,x₁+6x₄)

(1)求σ在基ε₁=(1,1,1,1),ε₂=(1,1,1,0),ε₃=(1,1,0,0),ε₄=(1,0,0,0)下的矩阵.

(2)判断σ是否为同构映射，并说明理由.

六、(10分)设A是n阶半正定矩阵，证明：|A+3E|≥3ⁿ.

七、(15分)设A为R上的3阶矩阵，且存在实列向量α使得α,Aα,A²α线性无关，而A³α=5A²α-6Aα，求|A³-3E|.

八、(15分，第1小题5分，第2小题10分)设P³ˣ³是数域P上全体3阶矩阵构成的线性空间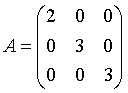，，W={B|AB=BA,B∈P³ˣ³}.

(1)证明W是子空间.(2)求子空间W的维数和一组基.

九、(15分)设A是数域P上的n阶方阵，A²=A. 令V₁和V₂分别为AX=0和(A-En)X=0的解空间，证明：Pⁿ=V₁⊕V₂.

十、(20分，第1小题12分，第2小题8分)

设三阶实对称矩阵.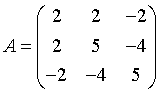

(1)求一个正交矩阵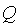及对角矩阵∧，使.

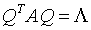(2)求一个对称矩阵P使A=P².

参考书目

北京大学数学系前代数小组. 高等代数. 高等教育出版社，2019年5月. 第5版.

以上就是考试大纲的具体内容，希望大家珍惜时间，合理安排考前的作息，预祝大家学有所成、金榜题名!