计算机考研知识点解析：数据结构之最小生成树

最小生成树(Minimum Spanning Tree ; MST) ：带权连通图中代价最小的生成树称为最小生成树。构造最小生成树的算法有许多，基本原则是：

(1)尽可能选取权值最小的边，但不能构成回路：一棵有n个顶点的生成树有且仅有n-1条边;如果一个图有n个顶点和小于n-1条边，则是非连通图;如果多于n-1条边，则一定有环;

(2)选择n-1条边构成最小生成树。

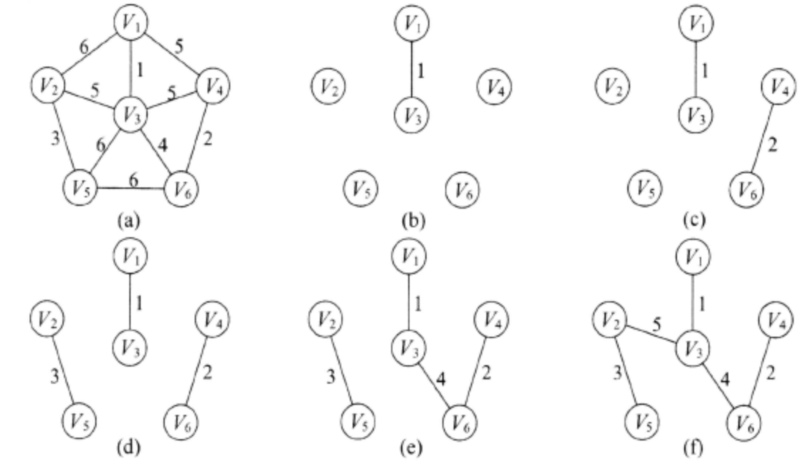
Prim算法：

(1)若从顶点v0出发构造，U={v0}，TE={};

(2)先找权值最小的边(u，v)，其中u∈U且v∈V-U，且子图不构成环，则U= U∪{v}，TE=TE∪{(u，v)};

(3)将U当成一个整体，先找权值最小的边(u，v)，其中u∈U且v∈V-U，且子图不构成环，则U= U∪{v}，TE=TE∪{(u，v)};请注意不管是到U中哪个顶点，只要权值最小都可以。

(4)重复(3)，直到U=V为止，此时则TE中必有n-1条边，T=(U，TE)就是最小生成树。

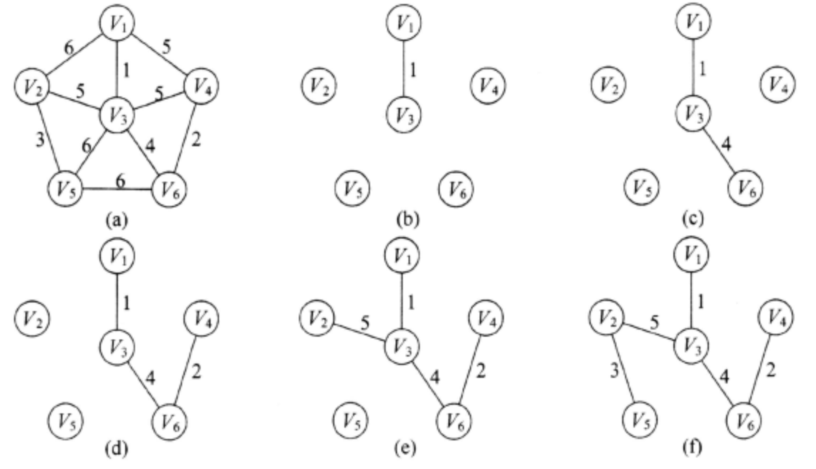
克鲁斯加尔算法：设G=(V, E)是具有n个顶点的连通网，T=(U, TE)是其最小生成树。初值：U=V，TE={} 。对G中的边按权值大小从小到大依次选取。

(1)选取权值最小的边(vi，vj)，若边(vi，vj)加入到TE后形成回路，则舍弃该边(边(vi，vj) ;否则，将该边并入到TE中，即TE=TE∪{(vi，vj)} 。

(2)重复(1)，直到TE中包含有n-1条边为止。

MST的一些性质：

(1)同一个算法(普利姆或者克鲁斯卡尔算法)最小生成树的构造过程是否唯一的

(2)不同算法(普利姆或者克鲁斯卡尔算法)最小生成树的构造过程是否唯一的

(3)不同算法(普利姆或者克鲁斯卡尔算法)构造的最小生成树是否是唯一的